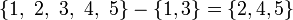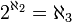Simboli Insiemistica
Abbiamo raccolto in questa pagina i Simboli Insiemistica per aiutarvi con una tabella facile da consultare nella vostra scoperta di questa affascinante teoria matematica. Come già detto, l'insiemistica è una disciplina che va a indagare la relazione tra i numeri, e che per questo motivo quando è stata sistematizzata in modo rigoroso (fatto che è avvenuto alla fine del XIX secolo ad opera del matematico tedesco Georg Cantor) ha avuto bisogno di inventare simboli che nuovi che descrivessero queste relazioni.
È così che sono nati i Simboli Insiemistica, che abbiamo raccolto qui per voi in una rapidissima guida, con tanto di esempi. Come potrete notare, alcuni simboli sono familiari a chiunque (come il per o il meno), mentre altri sono tipici di questa disciplina, come il simbolo di appartenenza, quello di cardinalità, quello di sottoinsieme di.
I simboli degli insiemi sono uno strumento fondamentale senza il quale questa disciplina non potrebbe esistere, e di conseguenza senza i quali la matematica sarebbe zoppa, manchevole di una base solida da cui partire.
Consultate la nostra guida agli insiemi simboli per studiare questa interessante branca della matematica.
| Simbolo | Come si legge | Funzionalità | Esempi |
|---|---|---|---|
 |
Meno | Differenza insiemistica o insieme complemento | 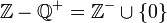
|
 |
Per | Prodotto cartesiano di insiemi | 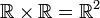 |
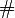 |
Cardinalità | Cardinalità di un insieme | 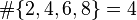 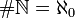 |
 |
Cardinalità | Cardinalità di un insieme | 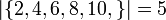 |
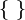 |
Insieme | Enumerano il contenuto di un insieme. |  |
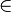 |
Appartiene | Appartenenza di un elemento ad un insieme |  |
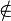 |
Non appartiene | Non appartenenza di un elemento ad un insieme | Se 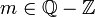 allora allora 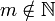 |
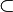 |
Sottoinsieme proprio di | Inclusione propria. Sottoinsieme proprio di un insieme dato | 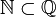 |
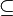 |
Sottoinsieme di | Inclusione. Sottoinsieme di un insieme dato (che può coincidere con l'insieme stesso) | 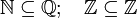 |
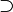 |
Soprainsieme proprio di | Soprainsieme proprio di un insieme dato | 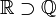 |
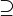 |
Soprainsieme di | Soprainsieme di un insieme dato (che può coincidere con l'insieme stesso) | 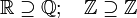 |
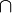 |
Intersecato | Intersezione insiemistica | 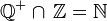 |
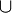 |
Unito | Unione insiemistica | 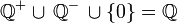 |
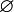 |
Insieme vuoto | Insieme vuoto | 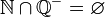 |
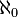 |
Aleph zero | Cardinalità degli insiemi numerabili | 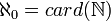 |
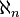 |
Aleph enne | Cardinalità dell'(n+1)-esimo numero transfinito secondo l'ipotesi generalizzata del continuo | 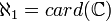
|
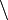 |
Meno | Differenza insiemistica o insieme complemento | 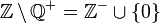 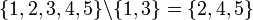 |
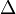 |
Differenza simmetrica | Differenza simmetrica fra insiemi | 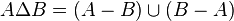 |