Insiemi Numerici
Alcuni insiemi, detti Insiemi numerici, hanno un ruolo particolarmente importante e pervasivo in tutte le branche della matematica:
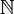- L'insieme dei Numeri naturali
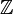- L'insieme dei Numeri interi
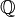- L'insieme dei Numeri razionali
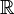- L'insieme dei Numeri reali
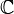- L'insieme dei Numeri complessi
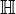- L'insieme dei Quaternioni
Questi insiemi, si possono vedere intuitivamente come contenuti uno nell'altro:
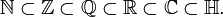
Cosa sono gli insiemi numerici
Come già detto, alcune nozioni dell'insiemistica rappresentano la vera e propria base della matematica. È il caso degli Insiemi Numerici. Se un insieme è una collezione di oggetti, un insieme numerico è una collezione di numeri, suddivisi a seconda delle loro caratteristiche. In questa pagina vogliamo darvi una breve guida per i più importanti gruppi di numeri:
Numeri naturali
L'espressione Numero naturale indica l'insieme dei numeri interi non negativi.
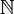= {0, 1, 2, 3, 4, 5, 6, 7, 8, ...}.
Numeri interi
I numeri interi sono formati dall'unione dei numeri naturali (0, 1, 2, 4, 5, 6...) e dei numeri interi negativi (−1, −2, −3, -4, -5, ...).Numeri razionali
Un numero razionale è un numero ottenibile come rapporto tra due numeri interi, il secondo dei quali diverso da 0 (Zero). Ogni numero razionale quindi può essere espresso mediante una frazione x/y, di cui a è detto il numeratore e y il denominatore.
Esempio: 1, 4, -3 , 4/5.
I numeri irrazionali
All'interno dei numeri reali, un altro insieme è quello dei numeri irrazionali. Essi sono quei numeri che non possono essere rappresentati da una frazione in cui numeratore e denominatore sono numeri interi e il denominatore non è zero. In forma decimale, questi numeri non hanno mai termine e non sono periodici. È un numero irrazionale ad esempio pi greco.
La scoperta dei numeri irrazionali si deve ai greci, che per primi capirono il fatto che alcuni numeri non hanno un sottomultiplo comune, e quindi sono incommensurabili.
I numeri reali
I numeri reali sono una fascia ampissima di numeri, che comprende tutti i numeri che possono avere uno sviluppo decimale sia esso finito o infinito. È quindi un numero reale ad esempio pi greco. E quindi i numeri reali possono essere positivi, negativi o anche nulli. La lettera che indica l'insieme dei numeri razionali è R.
Un'altra caratteristica dei numeri razionali è che essi possono essere messi in una corrispondenza biunivoca con i punti di una retta numerica.